UPSC CSAT Average PYQ with Solutions
Average Previous Questions (2011-2025) Solved
Struggling with Average questions in CSAT?
Learn smart shortcut techniques with solved PYQs (2011–2025) and clear explanations to improve speed and accuracy.
Year-wise Analysis of Average PYQs (2011–2025)
Q1. Consider a set of 11 numbers:
Value-I = Minimum value of the average of the numbers of the set when they are consecutive integers >= -5.
Value-II = Minimum value of the product of the numbers of the set when they are consecutive non-negative integers.
Which one of the following is correct? [CSAT 2025]
(a) Value-I < Value-II
(b) Value-II < Value-I
(c) Value-I = Value-II
(d) cannot be determined due to insufficient data
Correct Answer: (c) Value-I = Value-II
Method 1: The Direct Calculation (Finding the Minimums)
This method involves testing the lowest possible boundaries provided by the constraints.
Step 1: Calculate Value-I
Constraint: 11 consecutive integers >= -5.
The Set: To get the minimum average, we start at the lowest possible number: {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}
The Average: For any odd number of consecutive integers, the average is the middle term.
Middle term (6th position) = 0.
Value-I = 0.
Step 2: Calculate Value-II
Constraint: 11 consecutive non-negative integers (>=0).
The Set: To minimize a product, we want the smallest numbers possible: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
The Product: Multiplying any series of numbers by zero results in zero.
0 X 1 X 2 …… X 10 = 0
Value-II = 0.
Conclusion: 0 = 0, so Value-I = Value-II.
Method 2: The Logical Property Method (Fastest for CSAT)
This method uses mathematical properties to find the values without writing out the full sets.
1. Symmetry Property (for Value-I):
An average of a consecutive set is minimized when the set is shifted as far left on the number line as possible.
The problem allows us to go down to -5.
A set of 11 numbers starting at -5 will end at 5 (since -5 + (11-1) = 5).
Because the set {-5…5} is perfectly symmetrical around the origin, the negative numbers cancel out the positive numbers, leaving the sum as 0.
Average = 0.
2. Zero-Product Property (for Value-II):
The product of non-negative integers (0, 1, 2, ….) is minimized when the smallest possible value is included.
The smallest non-negative integer is 0.
The “Zero-Product Property” states that if any factor in a product is zero, the entire product is zero.
Since we can choose a set of consecutive integers that includes 0 (the set starting at 0), the minimum product must be 0.
Product = 0.
Conclusion: Both logic paths lead to 0. Thus, Option (c) is correct.
Q2. A Question is given followed by two Statements 1 and II. Consider the Question and the Statements.
Question: If the average marks in a class are 60, then what is the number of students in the class?
Statement-1: The highest marks in the class are 70 and the lowest marks are 50.
Statement-II: Exclusion of highest and lowest marks from the class does not change the average.
Which one of the following is correct in respect of the above Question and the Statements? [CSAT 2024]
(a) The Question can be answered by using one of the Statements alone, but cannot be answered using the other Statement alone.
(b) The Question can be answered by using either Statement alone.
(c) The Question can be answered by using both the Statements together, but cannot be answered using either Statement alone.
(d) The Question cannot be answered even by using both the Statements together.
Correct Answer: (b) The Question can be answered by using either Statement alone.
Solution
Method 1: Algebraic Proof
Avg =60 Sum = 60n
Statement 2 says: (Sum – 70 -50)/(n-2) = 60
(60n – 120)/ (n – 2) = 60
60(n-2)/(n-2) = 60
60 = 60
This equation is true for any value of (greater than 2). We cannot solve for .
Method 2: Scenario Testing
Try n = 3 (Scores: 50, 60, 70). Avg = 60. Remove 50/70, remaining avg is 60. Works.
Try n = 5 (Scores: 50, 60, 60, 60, 70). Avg = 60. Remove 50/70, remaining avg is 60. Works.
Since both n=3 and n=5 work, we cannot determine the unique answer.
Answer: (d)
Q3. Consider the following:
Weight of 6 boys = Weight of 3 men = Weight of 7 girls = Weight of 4 women
If the average weight of the women is 63 kg, then what is the average weight of the boys? [CSAT 2024]
(a) 40 kg
(b) 42kg
(c) 45 kg
(d) 63 kg
Correct Answer: (b) 42kg
Solution
Method 1: Ratio Method
6B = 4W
Ratio of Boy’s weight to Woman’s weight B/W = 4/6 = 2/3
Woman’s Weight = 63
Boy’s Weight = 2/3 x 63 = 2 x 21 = 42
Method 2: Total Mass Equivalence
“Weight of 6 Boys = Weight of 4 Women”.
Weight of 1 Woman = 63 kg.
Weight of 4 Women = 4 x 63 = 252 kg
Therefore, Weight of 6 Boys = 252 kg.
Weight of 1 Boy = 252/6 = 42 kg.
Answer: (b)
Q4. For five children with ages a<b<c<d<e; any two successive ages differ by 2 years.
Question: What is the age of the youngest child?
Statement-1: The age of the eldest is 3 times the youngest.
Statement-2: The average age of the children is 8 years.
Which one of the following is correct in respect of the above Question and the Statements? [CSAT 2023]
(a) The Question can be answered by using one of the Statements alone, but cannot be answered using the other Statement alone.
(b) The Question can be answered by using either Statement alone.
(c) The Question can be answered by using both the Statements together, but cannot be answered using either Statement alone.
(d) The Question cannot be answered even by using both the Statements together.
Correct Answer: (b) The Question can be answered by using either Statement alone.
Solution
Method 1: Testing Statement 1
“Eldest is 3 times youngest.”
Ages are a,a + 2,a + 4,a + 6,a +8
a+8 = 3a -> 8 = 2a -> a = 4
We found the age. Sufficient.
Method 2: Testing Statement 2
“Average is 8.”
In an AP with 5 terms, Average = Middle Term
Middle term is a+4
a+4 = 8-> a = 4
We found the age. Sufficient.
Answer: (b) (Either is sufficient)
Q5. The average weight of A, B, C is 40 kg, the average weight of B, D, E is 42 kg and the weight of F is equal to that of B. What is the average weight of A, B, C, D, E and F? [CSAT 2022]
(a) 40.5 kg
(b) 40.8 kg
(c) 41 kg
(d) Cannot be determined as data is inadequate
Correct Answer: (c) 41 kg
Solution
Method 1: Algebraic Substitution
Sum (A+B+C) = 120
Sum (B+D+E) = 126
We know F=B . Substitute F into the second group:
Sum (F+D+E) = 126
Now add Group 1 and Modified Group 2:
(A+B+C) + (F+D+E) = 120+126 = 246
Avg = 246/6 = 41
Method 2: Average of Averages
(Only works if group sizes are equal).
Avg of Group 1 = Avg of Group 2 = 42
Since we effectively swapped B for F (and they are equal), the groups (A,B,C) and (F,D,E) are disjoint sets of 3.
Overall Avg = (40+42)/2 = 41
Answer: (c)
Q6. There are two Classes A and B having 25 and 30 students respectively. In Class-A the highest score is 21 and lowest score is 17. In Class-B the highest score is 30 and lowest score is 22. Four students are shifted from Class-A to Class-B.
Consider the following statements: [CSAT 2021]
1. The average score of Class-B will definitely decrease.
2. The average score of Class-A will definitely increase. Which of the above statements is/are correct?
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2
Correct Answer: (a) 1 only
Solution
Method 1: Range/Boundary Logic
Statement 1: Moving students from A (Max 21) to B (Min 22).
You are adding “low value” numbers (maximum 21) into a “high value” group (minimum 22). This must lower the average. (Correct).
Statement 2: Removing students from A.
If you remove the “smartest” students of A (scored 21), the average of A drops.
If you remove the “weakest” students of A (scored 17), the average of A rises.
Result is unpredictable. (Incorrect).
Method 2: Counter-Example
Imagine Class A has scores ${20, 20, 20} = Avg 20$. Move all of them. Class A is empty (or just one left). Logic fails.
Imagine Class A has ${17, 21, 21} = Avg = 19.6. Remove the 17. Remaining avg = 21$ (Increased).
Imagine Class A has ${17, 17, 21} = Avg = 18.3. Remove the 21. Remaining Avg = 17$ (Decreased).
Since it can go up or down, Statement 2 is false.
Answer: (a)
Q7. The average score of a batsman after his 50th innings was 46.4. After 60th innings, his average score increases by 2.6. What was his average score in the last ten innings? [CSAT 2020]
(a) 122
(b) 91
(c) 62
(d) 49
Correct Answer: (c) 62
Solution
Method 1: “Deficit Make-up” Logic
Target: The batsman wants his average to become 49 (which is 46.4+2.6).
In the last 10 innings, he must score 49 average PLUS enough to fix the “deficit” of the previous 50 innings.
Gap to fill runs 50 innings x 2.6 (increase) = 130 runs
These 130 runs must come from the last 10 innings.
Extra per inning = 130/10 = 13
Avg of last 10 = New Overall Avg(49) + 13 =62
Method 2: Total Sums
Total after 60 = 60 x 49 = 2940
Total after 50 = 50 x 46.4 = 2320
Run difference = 620
Average = 620/10 = 62
Answer: (c)
Q8. The average age of a teacher and three students is 20 years. If all the three students are of same age and the difference between the age of the teacher and each student is 20 years, then what is the age of the teacher? [CSAT 2020]
(a) 25 years
(b) 30 years
(c) 35 years
(d) 45 years
Correct Answer: (c) 35 years
Solution
Method 1: Deviation Logic
Avg = 20 People = 4
The Teacher is 20 years older than the students.
Imagine everyone is the student’s age (S ). The total sum would be 4S
The Teacher adds an “extra” 20 years to the group.
Distribute that extra 20 years among 4 people = 5 years boost to the average.
So, Avg ( 20) = S +5
S = 15 Teacher = 15 +20 =35
Method 2: Basic Algebra
3x + (x+20)/4 = 20
4x + 20 = 80
4x = 60 -> x = 15
Teacher = 15+20 =35
Answer: (c)
Q9. In a class, there are three groups A, B and C. If one student from group A and two students from group B are shifted to group C, then what happens to the average weight of the students of the class? [CSAT 2020]
(a) It increases
(b) It decreases
(c) It remains the same
(d) No conclusion can be drawn due to insufficient data.
Correct Answer: (c) It remains the same
Solution
Method 1: Closed System Logic
The “Class” includes Groups A, B, and C.
Moving students from A to C is an internal transfer.
No one left the school, no one entered. The Total Weight of the class is constant. The Total Number of Students is constant.
Therefore, the Average cannot change.
Method 2: Algebraic Sum
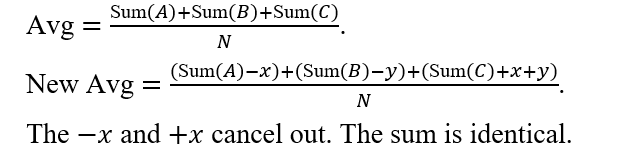
Answer: (c)
Q10. A family has two children along with their parents. The average of the weights of the children and their mother is 50 kg. The average of the weights of the children and their father is 52 kg. If the weight of the father is 60 kg, then what is the weight of the mother? (CSAT 2019)
(a) 48
(b) 50
(c) 52
(d) 54
Correct Answer: (d) 54
Solution
Method 1: Equation Subtraction
(Children + Mother) average = 50 kg for 3 people.
Total weight of children and mother:
50 × 3 = 150
(Children + Father) average = 52 kg for 3 people.
Total weight of children and father:
52 × 3 = 156
Subtract the two equations:
(Children + Father) − (Children + Mother)
Children cancel out.
Father − Mother = 156 − 150 = 6
Father is 6 kg heavier than Mother.
Given Father’s weight = 60 kg
Mother’s weight = 60 − 6 = 54 kg
Method 2: Average Gap Logic
When Mother is replaced by Father, the average weight increases
from 50 kg to 52 kg.
Increase in average = 2 kg
Number of people = 3
Increase in total weight = 3 × 2 = 6 kg
So, Father is 6 kg heavier than Mother.
Mother’s weight = 60 − 6 = 54 kg
Answer: (d)
Q11. The average marks of 100 students are given to be 40. It was found later that marks of one student were 53 which were misread as 83. The corrected mean marks are (CSAT 2019)
(a) 39
(b) 39.7
(c) 40
(d) 83, 89, 91, 97
Correct Answer: (d) 83, 89, 91, 97
Solution
Method 1: The “Prime Audit”
We need to check whether every number in a group is a prime number.
If even one number can be divided by another number, that group becomes the
different one.
Analyze the groups:
Group (a): 17, 37, 47, 97
All numbers are prime.
Group (b): 31, 41, 53, 67
All numbers are prime.
Group (c): 71, 73, 79, 83
All numbers are prime.
Group (d): 83, 89, 91, 97
83, 89, and 97 are prime numbers.
91 is not a prime number. It is a composite number.
91 = 7 × 13
Since Group (d) contains a non-prime number (91), it is the odd one out.
Method 2: The “Fake Prime” Detection
In exams, verifying every number takes time. Instead, look for
fake primes.
These numbers appear prime because they are odd and do not end in 5,
but they are actually composite.
The strategy:
Common tricky composite numbers in CSAT include:
51 = 17 × 3
57 = 19 × 3
87 = 29 × 3
91 = 13 × 7 (very common CSAT trap)
Applying the strategy:
1. Scan the options quickly.
2. Check whether numbers like 51, 57, 87, or 91 appear.
3. Here, 91 appears in option (d).
Quick verification:
Divisible by 3? → 9 + 1 = 10 (No)
Divisible by 7? → 7 × 13 = 91 (Yes)
Since 91 is divisible by 7, option (d) is the correct answer.
Q12. The average rainfall in a city for the first four days was recorded to be 0.40 inch. The rainfall on the last two days was in the ratio of 4:3. The average of six days was 0.50 inch. What was the rainfall on the fifth day? (CSAT 2017)
(a) 0.60 inch
(b) 0.70 inch
(c) 0.80 inch
(d) 0.90 inch
Correct Answer: (c) 0.80 inch
Solution
Method 1: Total Sum Subtraction
Total rainfall for 6 days:
6 × 0.50 = 3.00
Total rainfall for first 4 days:
4 × 0.40 = 1.60
Remaining rainfall for Day 5 and Day 6:
3.00 − 1.60 = 1.40
The rainfall of Day 5 and Day 6 is in the ratio 4 : 3.
Total ratio parts = 4 + 3 = 7
Rainfall on Day 5:
1.40 × (4 / 7) = 0.80
Method 2: Unitary Method
Let the value of one share in the ratio 4 : 3 be x.
Total shares = 7x
7x = 1.40
x = 0.20
Rainfall on Day 5 = 4 × 0.20 = 0.80
Answer: (c)
Q13. There are thirteen 2-digit consecutive odd numbers. If 39 is the mean of the first five such numbers, then what is the mean of all the thirteen numbers? (CSAT 2017)
(a) 47
(b) 49
(c) 51
(d) 45
Correct Answer: (a) 47
Solution
Method 1: The “Median” Shortcut
The mean of consecutive odd numbers is always the middle number.
For the first 5 numbers, the mean is 39.
This means the 3rd number is 39.
So the first five odd numbers are:
35, 37, 39, 41, 43
We now need the mean of all 13 numbers.
The middle position of 13 numbers is the 7th number.
Starting from the 3rd number (39), we move 4 steps forward.
Each step increases by 2.
39 + (4 × 2) = 39 + 8 = 47
Method 2: AP Formula
First, find the first term (a).
Mean of 5 terms = a + 4 = 39
So,
a = 35
Now calculate the mean of 13 terms.
Mean of an AP = a + ((n − 1) / 2) × d
Substitute values:
35 + (12 / 2) × 2
35 + 12 = 47
Answer: (a)
Q14. Suppose the average weight of 9 persons is 50 kg. The average weight of the first 5 persons is 45 kg, whereas the average weight of the last 5 persons is 55 kg. Then the weight of the 5th person will be (CSAT 2017)
(a) 45 kg
(b) 47.5 kg
(c) 50 kg
(d) 52.5 kg
Correct Answer: (c) 50 kg
Solution
Method 1: The “Overlap” Logic
Concept: There are 9 people in total.
Group A includes persons 1 to 5.
Group B includes persons 5 to 9.
The 5th person appears in both groups and is counted twice.
Hence, the formula becomes:
(Sum of first 5) + (Sum of last 5) = (Total sum of 9) + (5th person)
Substituting values:
(5 × 45) + (5 × 55) = (9 × 50) + X
225 + 275 = 450 + X
500 = 450 + X
X = 50
Method 2: Deviation Method
Overall average = 50
Average of first 5 = 45
Deviation = −5
Total deviation of first group:
5 × (−5) = −25
Average of last 5 = 55
Deviation = +5
Total deviation of second group:
5 × (+5) = +25
Net deviation = −25 + 25 = 0
Since the net deviation is zero, the overlapping person must be exactly
equal to the overall average.
X = 50
Answer: (c)
Q15. The average monthly income of a person in a certain family of 5 is Rs. 10,000. What will be the average monthly income of a person in the same family if the income of one person increased by Rs. 1,20,000 per year? (CSAT 2016)
(a) Rs. 12,000
(b) Rs. 16,000
(c) Rs. 20,000
(d) Rs. 34,000
Correct Answer: (a) Rs. 12,000
Solution
Method 1: The “Surplus Distribution” Shortcut
Logic: Do not calculate the full yearly income.
Focus only on the extra money added.
Extra annual income = 1,20,000
Extra monthly income = 1,20,000 ÷ 12 = 10,000
This extra 10,000 is distributed equally among 5 family members.
Change in average = 10,000 ÷ 5 = 2,000
New average income = 10,000 + 2,000 = 12,000
Method 2: Standard Formula
Old total monthly income:
5 people × 10,000 = 50,000
New income added per month = 10,000
New total income = 50,000 + 10,000 = 60,000
New average income = 60,000 ÷ 5 = 12,000
Answer: (a)
Q16. The sum of the ages of 5 members comprising a family, 3 years ago was 80 years. The average age of the family today is the same as it was 3 years ago, because of an addition of a baby during the intervening period. How old is the baby? (CSAT 2016)
(a) 6 months
(b) 1 year
(c) 2 years
(d) 2 years and 6 months
Correct Answer: (b) 1 year
Solution
Method 1: The “Total Years” Approach
Step 1: Find the total age 3 years ago.
Total age = 80 years
Step 2: Add the aging process.
There are 5 people, and each grew older by 3 years.
Increase in total age = 5 × 3 = 15 years
Expected total age (without baby) = 80 + 15 = 95 years
Step 3: Find the actual total age (with baby).
Average remains the same at 16.
Number of people = 6.
Actual total age = 16 × 6 = 96 years
Step 4: Find the baby’s age.
Baby’s age = 96 − 95 = 1 year
Method 2: The “Frozen Average” Logic
If the average remains unchanged even after 3 years,
it means the increase caused by the adults must have been
offset by the baby.
Extra years added by adults:
3 years × 5 people = 15 years
To keep the average fixed at 16, the baby must reduce the
average by exactly 15 years.
So, the baby must be 15 years younger than the average age.
Baby’s age = 16 − 15 = 1 year
Answer: (b)
Q17. A group of 630 children is seated in rows for a group photo session. Each row contains three less children then the row in front of it. Which one of the following number of rows is not possible? (CSAT 2014)
(a) 3
(b) 4
(c) 5
(d) 6
Correct Answer: (d) 6
Solution
Method 1: The “Parity / Integer Check”
Logic: You cannot have half a child. The number of children in the first row (a)
must be a whole number (an integer).
Formula used:
Total Sum = n / 2 × (First Row + Last Row)
Let us check option (d): 6 rows.
If there are 6 rows, the average number of children per row is:
630 ÷ 6 = 105
In an arithmetic progression with an even number of terms (6),
the average lies exactly between the two middle rows
(Row 3 and Row 4).
The difference between rows is 3, which is an odd number.
To average to 105, the middle values would have to be:
103.5 and 106.5
This gives fractional children, which is impossible.
Therefore, 6 rows is not possible.
Method 2: The Sum Formula
Use the arithmetic progression sum formula:
Sn = n / 2 [ 2a + (n − 1)d ]
Given:
Total sum = 630
Number of rows n = 6
Common difference d = −3
Substituting:
630 = 6 / 2 [ 2a + (6 − 1)(−3) ]
630 = 3 [ 2a − 15 ]
210 = 2a − 15
225 = 2a
a = 112.5
Since the first row cannot have a fractional number of children,
this case is not possible.
Answer: (d)
Q18. A student on her first 3 tests received an average score of N points. If she exceeds her previous average score by 20 points on her fourth test, then what is the average score for the first 4 tests? (CSAT 2011)
(a) N + 20
(b) N + 10
(c) N + 4
(d) N + 5
Correct Answer: (d) N + 5
Solution:
Method 1: The “Surplus Distribution” Approach
Think of average as equal sharing.
The student already has an average of N.
On the 4th test, she scores the same average (N) plus an extra 20 points
(N + 20).
The logic:
If she had scored exactly N, the average would not change.
The only reason the average changes is because of the extra surplus of 20 points.
To find the new average, distribute this extra surplus equally among all 4 tests.
Extra points = 20
Total tests = 4
Share per test = 20 ÷ 4 = 5
New average = N + 5
Answer: N + 5
Method 2: The “Substitution” Strategy
If algebra using N feels confusing, replace N with a real number.
This is a reliable CSAT technique.
Step 1: Choose an easy value.
Let N = 100.
Step 2: Calculate the totals.
First 3 tests:
Average = 100
Total score = 3 × 100 = 300
Fourth test score:
100 + 20 = 120
Step 3: Find the new average.
New total = 300 + 120 = 420
Total tests = 4
New average = 420 ÷ 4 = 105
Step 4: Match with options.
(a) N + 20 → 120 (Wrong)
(b) N + 10 → 110 (Wrong)
(c) N + 4 → 104 (Wrong)
(d) N + 5 → 105 (Correct)
Method 3: The “Total Sum” Approach
This method focuses on total scores rather than individual tests.
Average of first 3 tests = N
Sum of first 3 tests = 3 × N = 3N
Fourth test score = N + 20
New total sum = 3N + (N + 20) = 4N + 20
New average = (4N + 20) ÷ 4
Simplifying:
4N ÷ 4 + 20 ÷ 4 = N + 5
Therefore, the new average is N + 5.